Geometría y fotografía

Al leer el título de este artículo probablemente hayas pensado «No me gustan las matemáticas, ¡yo quiero hacer fotos!». Pero tenemos que asumir que geometría y fotografía están íntimamente ligadas porque una fotografía es un rectángulo: una visión enmarcada de la realidad. Por tanto, los elementos que se coloquen dentro de ese marco han de regirse por las reglas geométricas que ejercen los lados del rectángulo.

División del rectángulo

Cualquier elemento que coloquemos dentro del encuadre, por pequeño que sea, divide ese rectángulo. En teoría, podríamos dividir de cualquier manera, sin ningún tipo de limitación. Sin embargo, las divisiones más interesantes y que mejor funcionan son las que mantienen entre ellas una relación de proporcionalidad.

Varios pintores del renacimiento se dieron cuenta de que las divisiones basadas en número simples –1:1, 2:1, 3:2– producían divisiones estáticas. Para conseguir divisiones dinámicas hacían falta otras relaciones de división.

Proporción áurea

En la Grecia clásica se descubrió que en muchos elementos de la naturaleza se encontraba una de las divisiones más armónicas: la áurea. La razón de su armonía se debe a que todas las áreas de su división están relacionadas.

Esta relación, formulada en el siglo III aC por Euclides, dice que si dividimos un segmento en dos partes, podemos observar que la proporción entre la parte menor y la parte mayor era igual a la proporción existente entre la parte mayor y el total (es decir, la suma de ambas).

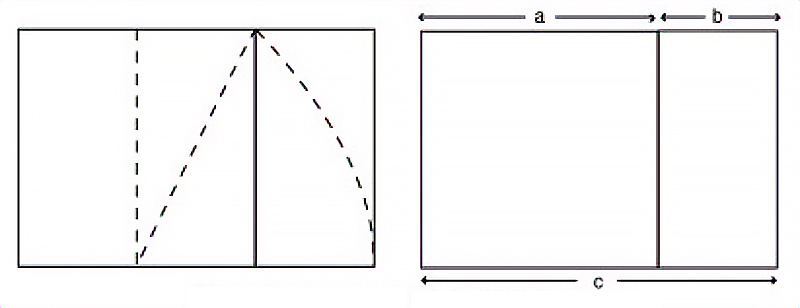
La proporción áurea se emplea desde entonces por arquitectos y artistas visuales para determinar la composición en todas las escalas: desde la forma de una página hasta la fachada de un edificio.

A este número se le llama número de oro, se representa por el símbolo ψy su valor es 1,61803… Otra propiedad de este rectángulo es que si se colocan dos iguales, se forma otro rectángulo áureo más grande.

Unos siglos más tarde, el matemático italiano Leonardo Fibonacci desarrolló una secuencia numérica según la cual cada número es la suma de los precedentes. Por ejemplo: 0 1 1(1+0) 2(1+1) 3(1+2) 5(2+3) 8(3+5) 13(5+8). Los cocientes entre dos números de esta sucesión se aproximan al número áureo.

Esta sucesión de números aparece en la naturaleza en diversas formas: Las escamas de una piña (el número de espirales de una piña siempre es igual a uno de los números de la sucesión), en el estudio de las leyes mendelianas de la herencia, en la formación de la concha de algunos moluscos… y, como no, en el diseño.

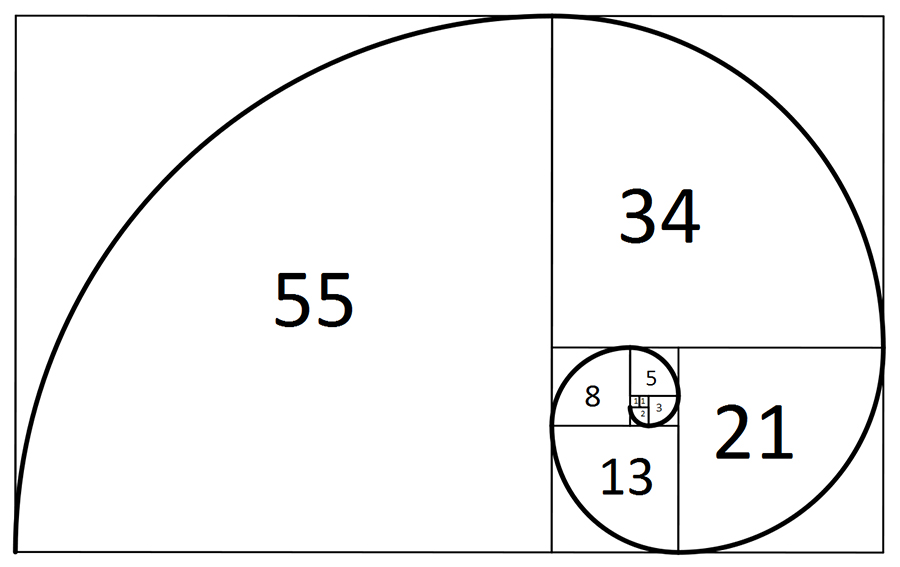
La famosa espiral áurea se construye utilizando esta progresión. Para ello, se empieza trazando un cuadrado de 1 unidad de lado –el nº 1–, se añade otro igual para formar un rectángulo de 2 x 1. A continuación añadimos un cuadrado de 2 x 2 –el nº 3– para formar un rectángulo de 3 x 2; después un cuadrado de 3 x 3 –el nº 4–, de manera que el siguiente rectángulo es 5 x 3, el siguiente cuadrado es 5 x 5 –el nº 5–, y así sucesivamente.

¿Y en las fotos?

Hasta aquí hemos tratado de explicarte por qué las cuestiones teóricas en las que se basan las relaciones entre geometría y fotografía. En el capítulo siguiente te explicaremos de qué manera influye esto en nuestras fotos. También veremos cómo aplicarlo para lograr que nuestras imágenes provoquen un mayor impacto visual.